从以上列举的三种情况看,我们发现,前、后两个数码之和相等的号码,如果用到1个数字,就有1个号码,即12个;用到2个数字,就有4个号码,即22;用到3个数字,就有9个号码,即32个。
前面已经说了,前、后两个数码之和最小的是0,最大的是18,共有19种情况。我们把这19种情况,即用到数字的个数及号码的数,列成下表。
从上表不难看出,前两个数码之和与后两个数之和相等的号码共有
(12+22+32+42+52+62+72+82+92)×2+102
=(1+4+9+16+25+36+49+64+81)×2+100
=285×2+100
=570+100
=670(个)
于是得出,除局号外,在其余的四个数码中,前两个数码之和与后两个数码之和不相等的电话号码共有
10000-670=9330(个)
答:前两个数码之和与后两个数码之和不相等的电话号码共有 9330个。
例99 用红、黄、蓝三种颜色把图57中8个圆圈涂上颜色,每个圆圈只许涂一种颜色,并且有连线的两端的圆圈不能涂上相同的颜色,那么共有多少种不同的涂法?
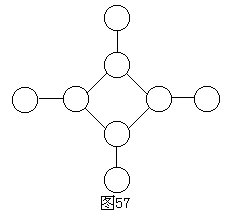
分析与解 根据题中条件,首先要想到中间菱形的四个圆圈连线最多,应该从这里开始思考。为了说明方便,先用字母表示图中各圆圈,如图58所示。
假如在A圆圈内涂红色,那么B、C、D三个圆圈的涂色方法有六种,如图59所示。
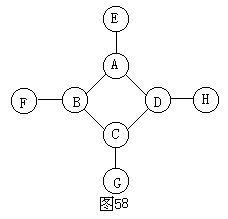
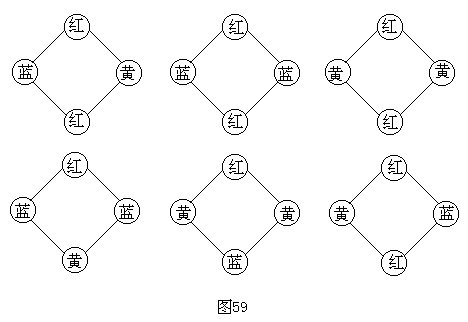
因为A圆圈可以涂红、黄、蓝三种颜色,所以A、B、C、D四个圆圈的涂色方法共6×3=18种。
又因为A、B、C、D都有一条线分别与E、F、G、H相连,所以 E、F、 G、H各有2种不同的涂法,由此共有18×2×2×2×2=288种不同的涂法。
答:共有288种不同的涂法。
例100 9月1日开学那天,五年级数学科代表向李老师汇报说:“李老师,我们100个同学,在暑假里一共做了1600道数学题。”李老师听了非常高兴,当即表扬了他们,并且说:“你们100个人中,至少有4个人做的数学题的数目一样多。”李老师说的这句话对吗?为什么?
分析与解 根据题意,把100个学生按3人为一组,分成33组,还剩下1个学生。
假设第1组3个学生都没做题,即每人做了0道题;第2组3个学生每人做1道题;第3组3个学生每人做2道题;…… 第33组3个学生每人做32道题。剩下的一个学生要是与前面的99个学生做的题数不相同,最少也要做33道题。这样100个学生最少共做了
3×(0+1+2+3+4+…+31+32)+33
=3×528+33
=1584+33
=1617(道)
超过了1600道题。要是不超过1600道题,必须有1个或更多的学生少做题,合起来共少做了17道题。其实只要有1个学生少做了题,这个学生就会归到其它做题少的那组中去。这样一来,那个组就会有4个学生做题一样多了。
因此,李老师的话是正确的。
,小学数学趣题巧算百题百讲百练--杂题部分